Multivariate Linear Regression
Hypothesis $$ h_\theta(x) = \begin{bmatrix}\theta_0 \hspace{2em} \theta_1 \hspace{2em} … \hspace{2em} \theta_n \end{bmatrix} \begin{bmatrix}x_0 \newline x_1 \newline \vdots \newline x_n\end{bmatrix} = \theta^T x $$
Gradient Descent Practices
- Scaling or normalize the range (e.g. mean normalization)
- learning rate $\alpha$
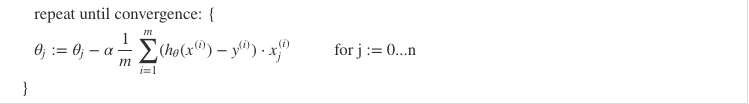
Ploynomial Regression
typical equations:
- $\theta_0x_0 + \theta_1x_1 + \theta_2x_2^2$
- $\theta_0x_0 + \theta_1x_1 + \theta_2x_2^2 + \theta_3x_3^3$
- $\theta_0x_0 + \theta_1x_1 + \theta_2 \sqrt{x_2}$
Normal Equation
if n > 1000, hard to solve the inverse of $(X^TX)^{-1}$
possible problem for inverstible
- redudant feature
- n>m