Diagram
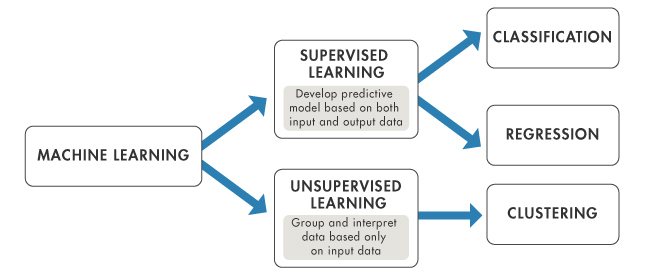
Supervised Learning
In supervised learning, we are given a data set and already know what our correct output should look like, having the idea that there is a relationship between the input and the output.
Supervised learning problems are categorized into “regression” and “classification” problems. In a regression problem, we are trying to predict results within a continuous output, meaning that we are trying to map input variables to some continuous function. In a classification problem, we are instead trying to predict results in a discrete output. In other words, we are trying to map input variables into discrete categories.
- regression => continuous value (predict housing price)
- classificiation => discrete value (yes, no)
note: infinitie attributes Support Vector Machine
Unsupervised Learning
Unsupervised learning allows us to approach problems with little or no idea what our results should look like. We can derive structure from data where we don’t necessarily know the effect of the variables.
- Clustering => (google news, DNA)
Cost Function
exmaple to take
Gradient Descent

concerns: local minimal, control of rate $\alpha$, cost if training data is big

Linear Algebra
- $A_{ij}$ refers to the element in the ith row and jth column of matrix A.
- A vector with ‘n’ rows is referred to as an ‘n’-dimensional vector. vi refers to the element in the ith row of the vector.
- Matrices are usually denoted by uppercase names while vectors are lowercase.
- “Scalar” means that an object is a single value, not a vector or matrix.
- ℝ refers to the set of scalar real numbers.
- ℝ𝕟 refers to the set of n-dimensional vectors of real numbers.
- vector => nx1 matrix
- Matrices are not commutative: A∗B≠B∗A
- Matrices are associative: (A∗B)∗C=A∗(B∗C)
- $ \begin{bmatrix} a & b \newline c & d \newline e & f \end{bmatrix} *\begin{bmatrix} x \newline y \newline \end{bmatrix} =\begin{bmatrix} a*x + b*y \newline c*x + d*y \newline e*x + f*y\end{bmatrix} $
Octave & Matlab
https://www.gnu.org/software/octave/
Glossary
tangent line
切线

reciprocal
倒数

derivative
求导
scalar
标量
having only magnitude, not direction.
versus vector has both magnitude & direction

polynomial
多项式
maligant
tending to invade normal tissue or to recur after removal; cancerous
benign
not harmful in effect: in particular, (of a tumor) not malignant.
cohesive

slope
斜率